Game Theory of the NovaBank Protocol

The NovaBank protocol is an innovation in how people interact with financial protocols.

We believe that NovaBank is so problem of creating a new currency through internal coordination among different stakeholders within the protocol, without resorting to any policies enforced by a central entity. Essentially, this is an example of the Prisoner's Dilemma. The Prisoner's Dilemma is a situation where individuals' personal interests conflict with a common goal, leading players in the game to not cooperate, even though cooperation is in their best interest.

We will first outline the basic elements of game theory and analyze the Prisoner's Dilemma from a purely abstract perspective. Then, we will delve into the specific components of NovaBank. NovaBank is a complex protocol that deserves an in-depth and thorough analysis.

The Prisoner's Dilemma

The first game that students of game theory learn is the Prisoner's Dilemma. This is because it is a simple game applicable to a variety of strategic situations. Once you see and understand it, you'll notice it everywhere.

The story goes like this: Two thieves plan to rob a store. As they approach the entrance, the police arrest them for illegal trespassing. The police suspect that the pair intended to rob the store, but they lack evidence to prove it. Therefore, they seek confessions to charge the suspects with a more serious crime. The interrogators separate the suspects and tell them:

"We are charging you with illegal trespassing, which will get you one month in jail. I know you planned to rob the store, but I can't prove it without your testimony. Now, confess to me, and I will dismiss your trespassing charge and set you free. Your friend will be charged with attempted robbery and face 12 months in jail. I am offering your friend the same deal. If you both confess, your individual testimonies will no longer be valuable, and you will both be sentenced to 8 months in jail."

Both players are self-interested and want to minimize their jail time. What should they do?

Using a payoff matrix allows us to condense all the information into an easily analyzable chart:

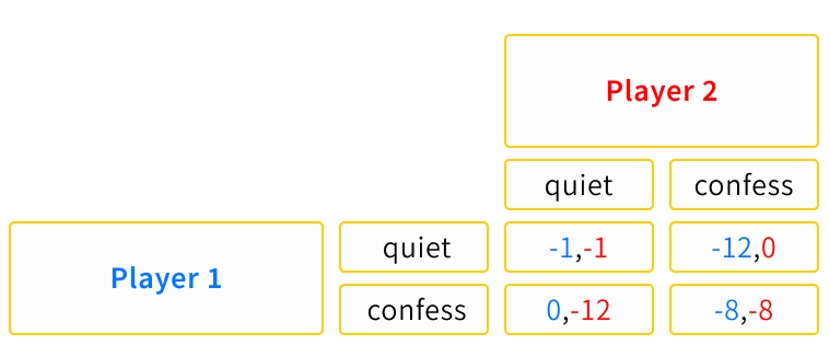
Player 1's available strategies are the rows (remain silent or confess), and their corresponding payoffs are the first number in each cell. Player 2's available strategies are the columns, and their corresponding payoffs are the second number in each cell.

quiet ； confess ； Blue numbers represent Player 1's payoffs, red numbers represent Player 2's payoffs ； -1: 1 month of imprisonment ； -8: 8 months of imprisonment ； -12: 12 months of imprisonment；0: acquittal (no imprisonment)；

Assumptions and Conclusions:

• We assume that both players prefer to minimize their jail time.

• We assume both players are selfish (i.e., they do not care about the fate of the other).

• We assume there is only one interaction.

• We assume the players cannot interact and plan their responses in advance.

These assumptions lead to a suboptimal outcome in the game: (confess, confess), which results in (-8, -8). We can see that if both players remain silent, they would receive less jail time. However, this is an unstable equilibrium because if both believe the other will stay silent, they are tempted to confess.

Therefore, (confess, confess) is the only Nash Equilibrium. A Nash Equilibrium is a state in a game where, given what the other players are doing, no player wants to deviate from their strategy.

However, if both players could cooperate and remain silent, they would achieve a better outcome. This is an important conclusion because it shows that two individuals may choose not to cooperate, even though it appears to be the best strategy for both.

Overcoming the Prisoner's Dilemma has significant implications for society at large and for NovaBank. We are often told that in a capitalist economy, individuals only care about their own interests, so selfish and competitive behavior is the norm, whereas cooperation is actually the best way to succeed.

NovaBank Game Theory Explanation

In the simplest NovaBank model, there are two players and three possible actions:

• Stake NVB

• Buy Bonds

• Sell NVB

When NVB staking rewards increase and the NVB price rises, players are more inclined to stake NVB. When players predict that staking rewards will decrease and the price will drop, they are most likely to sell NVB. When players are not significantly negatively impacted and have no clear inclination, they prefer to buy bonds (since bonds are discounted and offer arbitrage opportunities; the bond discounts will be detailed in the third part of the white paper on bond contracts).

Staking NVB can push the price up by +2, while selling NVB depresses the price by -2. Players engaging in NVB trading can gain a 50% profit. Buying bonds without staking NVB does not affect the price, but because bonds are discounted, the profit is +1.

From the table above, we can see that the optimal strategy is for both players to cooperate, with both staking, resulting in a payoff of 6. If one buys bonds and the other stakes, the result is 4. Selling/staking and selling/buying bonds offset each other, resulting in a neutral payoff of 0. The worst outcome is when both players distrust each other and rush to sell, resulting in -6.

Players' behavior depends on premiums, market prospects, macroeconomic environment, and a series of other factors. There's no need to pay too much attention to the size or sign of the numbers; the table is merely to illustrate the positive environment created by cooperation.

Mutual cooperation yields the best results. If you don't plan to stick around for the long term, we advise you not to participate. We don't need those who sell BTC at \$50,000 and buy back at \$30,000. Perhaps the NVB you hold is a better BTC.